Зададим декартову систему координат на плоскости. Изобразим комплексное число в его геометрической форме.
Угол $\varphi$ — аргумент числа $z$.

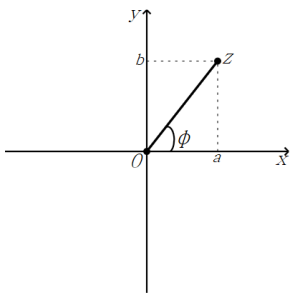
Между координатами точки существует взаимосвязь, которая верна при различных расположениях точек на плоскости:
$a=r\cos\varphi$, $b=r\sin\varphi$, где $r$ — это модуль комплексного числа $z$.
Эта взаимосвязь получена из определения геометрического представления комплексного числа.
Применив полученные формулы к алгебраической форме комплексного числа $\left(z=a+ib\right)$, мы получим: $z=a+ib=r\cos\varphi+i\left(r\sin\varphi\right)$, таким образом:
$z=r\left(\cos\varphi+i\sin\varphi\right)$ — тригонометрическая форма комплексного числа $z$.

Замечание!

Следует различать запись числа в тригонометрической форме и форме на него похожей:
$z=r\left(\cos\varphi-i\sin\varphi\right)$ — не тригонометрическая форма комплексного числа;
$z=r\left(\sin\varphi+i\cos\varphi\right)$ — не тригонометрическая форма комплексного числа;
$z=r\left(\cos\left(-\varphi\right)+i\sin\varphi\right)$ — не тригонометрическая форма комплексного числа.

Действия над комплексными числами в тригонометрической форме

$z_1=r_1\left(\cos\varphi_1+i\sin\varphi_1\right)$
$z_2=r_2\left(\cos\varphi_2+i\sin\varphi_2\right)$

Умножение

$z_1z_2=r_1r_2\left(\cos\varphi_1\cos\varphi_2-\sin\varphi_1\sin\varphi_2\right)+i\left(\cos\varphi_1\sin\varphi_2+\cos\varphi_2\sin\varphi_1\right)=$ $r_1r_2\left(\cos\left(\varphi_1+\varphi_2\right)+i\sin\left(\varphi_1+\varphi_2\right)\right)$

Деление

$\frac{z_1}{z_2}$=$\frac{r_1\left(\cos\varphi_1+i\sin\varphi_1\right)}{r_2\left(\cos\varphi_2+i\sin\varphi_2\right)}=$ $\frac{r_1}{r_2}\cdot\frac{\left(\cos\varphi_1+i\sin\varphi_1\right)\left(\cos\left(-\varphi_2\right)+i\sin\left(-\varphi_2\right)\right)}{\cos^{2}\varphi_2+\sin^{2}\varphi_2}=$ $\frac{r_1}{r_2}\left(\cos\left(\varphi_1-\varphi_2\right)+i\sin\left(\varphi_1-\varphi_2\right)\right)$

Возведение в степень (Формула Муавра)

$z\in\mathbb{C}$, $z=r\left(\cos\varphi+i\sin\varphi\right)$, $\forall n\in\mathbb{Z}$:
$z^{n}=r^{n}\left(\cos\left(n\varphi\right)+i\sin\left(n\varphi\right)\right)$

Тригонометрическое представление комплексных чисел

Лимит времени: 0

Навигация (только номера заданий)

0 из 4 заданий окончено

Вопросы:

1. 1
2. 2
3. 3
4. 4

Информация

Пройдите тест, чтобы узнать хорошо ли Вы поняли материал.

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается...

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Результаты

Правильных ответов: 0 из 4

Время вышло

Вы набрали 0 из 0 баллов (0)

Средний результат
Ваш результат

Рубрики

1. Нет рубрики 0%
2. Алгебра 0%

Ваш результат был записан в таблицу лидеров

Загрузка

Имя: E-Mail:

Капча:

максимум из 4 баллов

Место	Имя	Записано	Баллы	Результат
Таблица загружается
Нет данных

1. 1
2. 2
3. 3
4. 4

1. С ответом
2. С отметкой о просмотре

1. Задание 1 из 4

   1.

   Количество баллов: 1

   Какая запись является записью числа в его тригонометрической форме?

   • $\left(\sin \alpha+i\cos \alpha\right)$
   • $2\left(\cos 2\pi+i\sin 2\pi\right)$
   • $\sin 0-i\cos0$
   • $2\left(\sin \frac {\pi}{3}+i\cos \frac {\pi}{3}\right)$
   • $\left(\cos \frac{\pi}{2}+i\cos \frac{\pi}{2}\right)$
   • $2\left(\cos 8+i\sin 8\right)$
   Правильно
   

   Неправильно
   
2. Задание 2 из 4

   2.

   Количество баллов: 1

   Сопоставить комплексные числа в их алгебраической и тригонометрической формах.

   Элементы сортировки

   • $\cos\pi+i \sin\pi$
   • $\cos 2\pi k+i \sin 2\pi k$
   • $\sqrt{2}\left(\cos 2\pi k+i \sin 2\pi k\right)$
   • $\cos \frac{\pi}{2}+i \sin \frac{\pi}{2}$

   • -1

   • 1

   • 1-i

   • i

   Правильно
   

   Неправильно
   
3. Задание 3 из 4

   3.

   Количество баллов: 1

   В какую степень необходимо возвести число $=2\left(\cos \frac{\pi}{3}+i \sin \frac{\pi}{3}\right)$? чтобы получить: $=16\left(\cos \frac{4\pi}{3}+i \sin \frac{4\pi}{3}\right)$?
   Правильно
   

   Неправильно
   
4. Задание 4 из 4

   4.

   Количество баллов: 1

   $=\frac{\left(1-i\sqrt{3}\right)\left(\cos\varphi+i\sin\varphi\right)}{2\left(1-i\right)\left(\cos\varphi-i\sin\varphi\right)}$

   • $\frac{\sqrt{2}}{2}\left(\cos\left(\varphi-\frac{\pi}{12}\right)+i\sin\left(\varphi-\frac{\pi}{12}\right)\right)$
   • $\frac{\sqrt{2}}{2}\left(\cos\left(2\varphi-\frac{\pi}{12}\right)+i\sin\left(2\varphi-\frac{\pi}{12}\right)\right)$
   • $\frac{\sqrt{2}}{\sqrt{2}}\left(\cos\left(2\varphi-\frac{\pi}{6}\right)+i\sin\left(2\varphi-\frac{\pi}{6}\right)\right)$
   • $\frac{\sqrt{2}}{2}\left(\cos\left(-\frac{\pi}{12}\right)+i\sin\left(-\frac{\pi}{12}\right)\right)$
   • $\left(\cos\left(2\varphi-\frac{\pi}{12}\right)+i\sin\left(2\varphi-\frac{\pi}{12}\right)\right)$
   Правильно
   

   Неправильно
   

Список использованной литературы:

• Курош А.Г. Курс высшей алгебры. М.: Наука, 1968, Глава 4, § 18, «Дальнейшее изучение комплексных чисел» стр.117-118;
• Личный конспект, составленный на основе лекций Г.С.Белозерова
• Фаддеев Д.К. Лекции по алгебре. М.: Наука, 1984, Глава 2, §2, стр.31-39